 Introduction au langage de programmation Python
3
Introduction au langage de programmation Python
3
Ce cours a été testé sous Windows et GNU/Linux.
Python 2 . Python 3
Chapitre 4 - Les fonctions
Nous avons déjà vu beaucoup de fonctions : print(), type(), len(), input(), range()...
Ce sont des fonctions pré-définies (built-in functions).
Nous avons aussi la possibilité de créer nos propres fonctions !
Intérêt des fonctions
Une fonction est une portion de code que l'on peut appeler au besoin (c'est une sorte de sous-programme).
L'utilisation des fonctions évite des redondances dans le code : on obtient ainsi des programmes plus courts et plus lisibles.
Par exemple, nous avons besoin de convertir à plusieurs reprises des degrés Celsius en degrés Fahrenheit :
>>> print(100.0*9.0/5.0 + 32.0) 212.0 >>> print(37.0*9.0/5.0 + 32.0) 98.6 >>> print(233.0*9.0/5.0 + 32.0) 451.4
La même chose en utilisant une fonction :
>>> def fahrenheit(degre_celsius): """ Conversion degré Celsius en degré Fahrenheit """ print(degre_celsius*9.0/5.0 + 32.0) >>> fahrenheit(100) 212.0 >>> fahrenheit(37) 98.6 >>> temperature = 233 >>> fahrenheit(temperature) 451.4
Rien ne vous oblige à définir des fonctions dans vos scripts, mais cela est tellement pratique qu'il serait improductif de s'en passer !
L'instruction def
Syntaxe
def nom_de_la_fonction(parametre1, parametre2, parametre3, ...): """ Documentation qu'on peut écrire sur plusieurs lignes """ # docstring entouré de 3 guillemets (ou apostrophes) bloc d'instructions # attention à l'indentation return resultat # la fonction retourne le contenu de la variable resultat
Exemple n°1
# script Fonction1.py def mapremierefonction(): # cette fonction n'a pas de paramètre """ Cette fonction affiche 'Bonjour' """ print("Bonjour") return # cette fonction ne retourne rien ('None') # l'instruction return est ici facultative
Une fois la fonction définie, nous pouvons l'appeler :
>>> mapremierefonction() # ne pas oublier les parenthèses () Bonjour
L'accès à la documentation se fait avec la fonction pré-définie help() :
>>> help(mapremierefonction) # affichage de la documentation Help on function mapremierefonction in module __main__: mapremierefonction() Cette fonction affiche 'Bonjour'
Exemple n°2
La fonction suivante simule le comportement d'un dé à 6 faces.
Pour cela, on utilise la fonction randint() du module random.
# script Fonction2.py def tirage_de(): """ Retourne un nombre entier aléatoire entre 1 et 6 """ import random valeur = random.randint(1, 6) return valeur
>>> print(tirage_de()) 3 >>> print(tirage_de()) 6 >>> resultat = tirage_de() >>> print(resultat) 1
Exemple n°3
# script Fonction3.py # définition des fonctions def info(): """ Informations """ print("Touche q pour quitter") print("Touche Enter pour continuer") def tirage_de(): """ Retourne un nombre entier aléatoire entre 1 et 6 """ import random valeur = random.randint(1, 6) return valeur # début du programme info() while True: choix = input() if choix == 'q': break print("Tirage :", tirage_de())
>>> Touche q pour quitter Touche Enter pour continuer Tirage : 5 Tirage : 6 q >>>
Exemple n°4
Une fonction avec deux paramètres :
# script Fonction4.py # définition de fonction def tirage_de2(valeur_min, valeur_max): """ Retourne un nombre entier aléatoire entre valeur_min et valeur_max """ import random return random.randint(valeur_min, valeur_max) # début du programme for i in range(5): print(tirage_de2(1, 10)) # appel de la fonction avec les arguments 1 et 10
>>> 6 7 1 10 2 >>>
Exemple n°5
Une fonction qui retourne une liste :
# script Fonction5.py # définition de fonction def tirage_multiple_de(nombretirage): """ Retourne une liste de nombres entiers aléatoires entre 1 et 6 """ import random resultat = [random.randint(1, 6) for i in range(nombretirage)] # compréhension de listes (Cf. annexe) return resultat # début du programme print(tirage_multiple_de(10))
>>> [4, 1, 3, 3, 2, 1, 6, 6, 2, 5]
>>> help(tirage_multiple_de) Help on function tirage_multiple_de in module __main__: tirage_multiple_de(nombretirage) Retourne une liste de nombres entiers aléatoires entre 1 et 6
Exemple n°6
Une fonction qui affiche la parité d'un nombre entier.
Il peut y avoir plusieurs instructions return dans une fonction.
L'instruction return provoque le retour immédiat de la fonction.
# script Fonction6.py # définition de fonction def parite(nombre): """ Affiche la parité d'un nombre entier """ if nombre%2 == 1: # L'opérateur % donne le reste d'une division print(nombre, 'est impair') return if nombre%2 == 0: print(nombre, 'est pair') return
>>> parite(13) 13 est impair >>> parite(24) 24 est pair
Portée de variables : variables globales et locales
La portée d'une variable est l'endroit du programme où on peut accéder à la variable.
Observons le script suivant :
a = 10 # variable globale au programme def mafonction(): a = 20 # variable locale à la fonction print(a) return
>>> print(a) # nous sommmes dans l'espace global du programme 10 >>> mafonction() # nous sommes dans l'espace local de la fonction 20 >>> print(a) # de retour dans l'espace global 10
Nous avons deux variables différentes qui portent le même nom a
Une variable a de valeur 20 est créée dans la fonction : c'est une variable locale à la fonction.
Elle est détruite dès que l'on sort de la fonction.
global
L'instruction global rend une variable globale :
a = 10 # variable globale def mafonction(): global a # la variable est maintenant globale a = 20 print(a) return
>>> print(a) 10 >>> mafonction() 20 >>> print(a) 20
Remarque : il est préférable d'éviter l'utilisation de l'instruction global car c'est une source d'erreurs (on peut ainsi modifier le contenu d'une variable globale en croyant agir sur une variable locale).
La sagesse recommande donc de suivre la règle suivante :
- ne jamais affecter dans un bloc de code local une variable de même nom qu'une variable globale
Annexe : la compréhension de listes
La compréhension de listes est une structure syntaxique disponible dans un certain nombre de langages de programmation, dont Python.
C'est une manière de créer efficacement des listes.
Revenons sur l'exemple vu dans le script Fonction5.py :
resultat = [random.randint(1, 6) for i in range(10)]
>>> print(resultat) [3, 1, 5, 6, 4, 2, 1, 1, 3, 1]
Autre exemple : liste de carrés
carres = [i*i for i in range(11)]
>>> print(carres) [0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
La compréhension de listes évite donc d'écrire le code "classique" suivant :
carres = []
for i in range(11):
carres.append(i*i)
Exercices
Exercice 4.1 ☆
1) Ecrire une fonction carre() qui retourne le carré d'un nombre :
>>> print(carre(11.11111)) 123.4567654321
2) Avec une boucle while et la fonction carre(), écrire un script qui affiche le carré des nombres entiers de 1 à 100 :
>>> 1² = 1 2² = 4 3² = 9 ... 99² = 9801 100² = 10000 Fin du programme
Exercice 4.2 ☆
1) Ecrire une fonction qui retourne l'aire de la surface d'un disque de rayon R.
Exemple :
>>> print(airedisque(2.5)) 19.6349540849
2) Ajouter un paramètre qui précise l'unité de mesure :
>>> print(airedisque2(4.2, 'cm')) 55.4176944093 cm²
Exercice 4.3 ★
1) Ecrire une fonction qui retourne la factorielle d'un nombre entier N.
On rappelle que : N ! = 1×2×...×(N-1)×N
Exemple :
>>> print(factorielle(50)) 30414093201713378043612608166064768844377641568960512000000000000
2) Comparez avec le résultat de la fonction factorial() du module math.
Exercice 4.4 ★
1) A l'aide de la fonction randint() du module random, écrire une fonction qui retourne un mot de passe de longueur N (chiffres, lettres minuscules ou majuscules).
On donne :
chaine = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz'
>>> print(password(10)) mHVeC5rs8P >>> print(password(6)) PYthoN
2) Reprendre la question 1) avec la fonction choice() du module random.
Pour obtenir de l'aide sur cette fonction :
>>> import random >>> help(random.choice)
3) Quel est le nombre de combinaisons possibles ?
4) Quelle durée faut-il pour casser le mot de passe avec un logiciel capable de générer 1 million de combinaisons par seconde ?
Lien utile : www.exhaustif.com/Generateur-de-mot-de-passe-en.html
Exercice 4.5 ★ Ecrire une fonction qui retourne une carte (au hasard) d'un jeu de Poker à 52 cartes.
On utilisera la fonction choice() ou randint() du module random.
On donne :
ListeCarte = ['2s','2h','2d','2c','3s','3h','3d','3c','4s','4h','4d','4c','5s','5h','5d','5c',
'6s','6h','6d','6c','7s','7h','7d','7c','8s','8h','8d','8c','9s','9h','9d','9c',
'Ts','Th','Td','Tc','Js','Jh','Jd','Jc','Qs','Qh','Qd','Qc','Ks','Kh','Kd','Kc','As','Ah','Ad','Ac']
>>> print(tiragecarte()) 7s >>> print(tiragecarte()) Kd
Exercice 4.6 ★★
1) Ecrire une fonction qui retourne une liste de N cartes différentes d'un jeu de Poker à 52 cartes.
Noter qu'une fonction peut appeler une fonction : on peut donc réutiliser la fonction tiragecarte() de l'exercice précédent.
Exemple :
>>> print(tirage_n_carte(2)) ['As', 'Ah'] >>> print(tirage_n_carte(25)) ['Jc', 'Jh', 'Tc', '2d', '3h', 'Qc', '8d', '7c', 'As', 'Td', '8h', '9c', 'Ad', 'Qh', 'Kc', '6s', '5h', 'Qd', 'Kh', '9h', '5d', 'Js', 'Ks', '5c', 'Th']
2) Simplifier le script avec la fonction shuffle() ou sample() du module random.
Exercice 4.7 ★ Ecrire une fonction qui retourne une grille de numéros du jeu Euro Millions.
On utilisera la fonction sample() du module random.

>>> print(euromillions()) [37, 23, 9, 11, 49, 2, 11] >>> print(euromillions()) [16, 32, 8, 30, 40, 6, 4]
Exercice 4.8 ★★
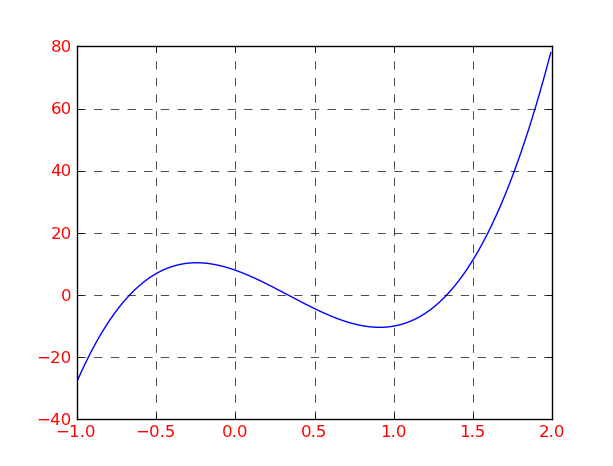
1) Ecrire une fonction qui retourne la valeur de la fonction mathématique f(x)= 27x3 -27x2 -18x +8 :
>>> print(f(0), f(1), f(0.5), f(0.25), f(0.375)) 8.0 -10.0 -4.375 2.234375 -1.123046875
2) On se propose de chercher les zéros de cette fonction par la méthode de dichotomie.
Ecrire le script correspondant.
>>> Recherche d'un zéro dans l'intervalle [a,b] a? 0 b? 1 Précision ? 1e-12 0.5 0.25 0.375 0.3125 0.34375 0.328125 0.3359375 0.33203125 0.333984375 0.3330078125 0.33349609375 0.333251953125 ... ... 0.333333333333 >>>
3) Chercher tous les zéros de cette fonction.
Annexe : représentation graphique de la fonction f(x)= 27x3 -27x2 -18x +8 (graphique réalisé avec la librairie matplotlib de Python)
QCM
Contenu sous licence CC BY-NC-SA 3.0
Fabrice Sincère ; version 1.5.11
Contacter l'auteur